Calculus for Machine Learning
This tutorial introduces the essential calculus concepts that power machine learning algorithms. You'll learn summation and product notation, derivatives for optimization, and integrals for probability—all with clear examples connecting math to ML practice.
Estimated time: 70 minutes
Why This Matters
Problem statement: Machine learning models learn by adjusting parameters to minimize errors. Without understanding derivatives (how functions change), gradients (direction of steepest change), and optimization (finding best parameters), you cannot grasp how models actually learn or why training sometimes fails.
Practical benefits: Calculus provides the mathematical framework for optimization algorithms like gradient descent, the backbone of neural network training. Understanding derivatives helps you debug vanishing gradients, tune learning rates, interpret loss curves, and implement custom training loops. Integrals appear in probability calculations and computing expected values for model evaluation.
Professional context: Every time a neural network trains, it's computing thousands of derivatives using the chain rule (backpropagation). Understanding calculus transforms "black box" training into something you can reason about, debug, and improve. When a model fails to converge or gradients explode, calculus knowledge helps you identify and fix the problem.

Prerequisites & Learning Objectives
Required knowledge:
- Algebra fundamentals (functions, equations, exponents)
- Basic understanding of graphs and coordinate systems
- Python basics for computational examples
- Completed Linear Algebra tutorial (vectors, matrices)
Learning outcomes:
- Read and write summation and product notation
- Understand what derivatives measure and why they matter for ML
- Apply derivative rules (sum, product, chain) to compute gradients
- Compute partial derivatives for multivariate functions
- Understand integrals as area under curves and cumulative sums
- Connect calculus concepts to gradient descent and backpropagation
Start with notation for sums and products, build intuition for derivatives as rates of change, master derivative rules used in ML, then understand integrals for probability and optimization.
Core Concepts
Why Calculus for Machine Learning?
Calculus is the mathematics of change and accumulation. Machine learning is fundamentally about:
- Understanding complex systems - how small input changes affect outputs
- Optimizing algorithms - finding parameter values that minimize loss
- Computing gradients - determining which direction improves the model
- Working with probability - integrating probability density functions
Training a model means repeatedly asking "if I change this parameter slightly, does my loss go up or down?" That question is answered by derivatives.
Calculus in the ML Workflow
| ML Task | Calculus Concept | Example |
|---|---|---|
| Model training | Derivatives | Gradient descent optimization |
| Backpropagation | Chain rule | Computing gradients layer-by-layer |
| Loss functions | Derivatives | Finding minimum prediction error |
| Probability | Integrals | Computing expected values, cumulative distributions |
| Feature analysis | Partial derivatives | Understanding feature sensitivity |
Summation Notation
Summation notation provides a compact way to express the sum of many terms—essential for expressing loss functions and aggregating predictions.
Sigma notation $\(\Sigma\)$:
The symbol $\(\Sigma\)$ (capital Greek sigma) means "sum up all these terms."
Breaking it down:
- $\(i\)$ is the index variable (usually starts at 1)
- $\(i=1\)$ is the starting value
- $\(n\)$ is the ending value (upper limit)
- $\(a_i\)$ is the term being summed (depends on $\(i\)$)
Example 1: Sum of first 10 integers
Example 2: Sum of squares
Python implementation:
import numpy as np
# Sum of first 10 integers
result = sum(range(1, 11))
print(f"Sum of 1 to 10: {result}")
# Sum of squares from 1 to 3
squares = [i**2 for i in range(1, 4)]
result = sum(squares)
print(f"Sum of squares: {result}")
# Using NumPy
arr = np.arange(1, 11)
print(f"NumPy sum: {np.sum(arr)}")
Expected output:
ML connection: The mean squared error (MSE) loss function is a summation:
This sums up squared errors across all $\(n\)$ data points.
Product Notation
Product notation uses $\(\Pi\)$ (capital Greek pi) to represent multiplication of multiple terms.
Pi notation $\(\Pi\)$:
Example 1: Product of first 5 integers (factorial)
Example 2: Nested products
Python implementation:
import numpy as np
# Product of first 5 integers
result = np.prod(range(1, 6))
print(f"Product of 1 to 5: {result}")
# Nested products
result = 1
for i in range(1, 3):
for j in range(1, 4):
result *= (i * j)
print(f"Nested product: {result}")
Expected output:
ML connection: Probability calculations often involve products. For example, the likelihood of independent events:
Common Mathematical Series
Certain series appear frequently in ML and have known formulas.
Faulhaber's formulas for power sums:
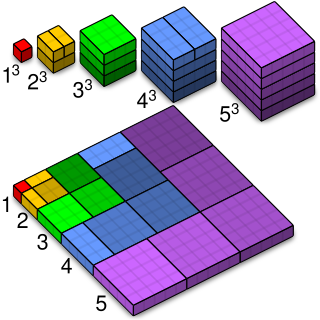
Sum of first $\(m\)$ integers:
Example: $\(\sum_{k=1}^{100} k = \frac{100 \cdot 101}{2} = 5050\)$
Sum of first $\(m\)$ squares:
Example: $\(\sum_{k=1}^{10} k^2 = \frac{10 \cdot 11 \cdot 21}{6} = 385\)$
Sum of first $\(m\)$ cubes:
Example: $\(\sum_{k=1}^{5} k^3 = \left[\frac{5 \cdot 6}{2}\right]^2 = 15^2 = 225\)$
Python verification:
import numpy as np
m = 10
# Sum of integers
formula_result = m * (m + 1) // 2
actual_result = sum(range(1, m + 1))
print(f"Sum of integers - Formula: {formula_result}, Actual: {actual_result}")
# Sum of squares
formula_result = m * (m + 1) * (2*m + 1) // 6
actual_result = sum([k**2 for k in range(1, m + 1)])
print(f"Sum of squares - Formula: {formula_result}, Actual: {actual_result}")
# Sum of cubes
formula_result = (m * (m + 1) // 2) ** 2
actual_result = sum([k**3 for k in range(1, m + 1)])
print(f"Sum of cubes - Formula: {formula_result}, Actual: {actual_result}")
Expected output:
Sum of integers - Formula: 55, Actual: 55
Sum of squares - Formula: 385, Actual: 385
Sum of cubes - Formula: 3025, Actual: 3025
Why these matter: Understanding series helps you analyze algorithm complexity and compute aggregate statistics efficiently.
What is a Derivative?
A derivative measures the rate of change of a function. It answers the question: "If I change the input by a tiny amount, how much does the output change?"
Formal definition:
This says: "Take the change in output $\((f(x+h) - f(x))\)$, divide by the change in input $\((h)\)$, and see what happens as $\(h\)$ gets infinitely small."
Geometric interpretation: The derivative is the slope of the tangent line to the function at a point.

Notation variations:
- $\(f'(x)\)$ (prime notation)
- $\(\frac{df}{dx}\)$ (Leibniz notation)
- $\(\frac{dy}{dx}\)$ (when $\(y = f(x)\)$)
Example: Derivative of $\(f(x) = x^2\)$
Using the definition:
So $\(\frac{d}{dx}(x^2) = 2x\)$.
Physical intuition: If $\(f(x)\)$ is position, $\(f'(x)\)$ is velocity. If $\(f(x)\)$ is velocity, $\(f'(x)\)$ is acceleration.
ML connection: In gradient descent, the derivative tells us which direction to move parameters to reduce loss.
Common Derivative Rules
Instead of using the limit definition every time, we use standard rules.
Power rule:
Examples:
-
\[\frac{d}{dx} x^3 = 3x^2\]
-
\[\frac{d}{dx} x^{10} = 10x^9\]
-
\[\frac{d}{dx} \sqrt{x} = \frac{d}{dx} x^{1/2} = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}}\]
Constant rule:
Constants don't change, so their rate of change is zero.
Linear function:
The slope of a line is constant.
Logarithm:
Exponential:
The exponential function is its own derivative!
Reciprocal:
Python verification:
import numpy as np
import matplotlib.pyplot as plt
# Function f(x) = x^2
def f(x):
return x**2
# Derivative f'(x) = 2x
def f_prime(x):
return 2*x
# Numerical derivative approximation
def numerical_derivative(f, x, h=1e-5):
return (f(x + h) - f(x)) / h
# Test at x = 3
x = 3
analytical = f_prime(x)
numerical = numerical_derivative(f, x)
print(f"Analytical derivative at x={x}: {analytical}")
print(f"Numerical derivative at x={x}: {numerical:.6f}")
Expected output:
Sum Rule for Derivatives
When functions are added, their derivatives add.
Sum rule:
Example:
ML connection: Loss functions are often sums of individual errors across data points:
The derivative is:
This is why we can compute gradients for mini-batches and sum them.
Product Rule for Derivatives
When functions are multiplied, the derivative follows a specific pattern.
Product rule:
Mnemonic: "First times derivative of second, plus second times derivative of first."
Example:
Let $\(f(x) = x^2\)$ and $\(g(x) = \sin(x)\)$.
Why not just $\(f'(x) \cdot g'(x)\)$? Because multiplication is not a linear operation. The product rule accounts for how both functions change together.
Python verification:
import numpy as np
# Function h(x) = x^2 * e^x
def h(x):
return x**2 * np.exp(x)
# Derivative using product rule: h'(x) = 2x * e^x + x^2 * e^x
def h_prime(x):
return 2*x * np.exp(x) + x**2 * np.exp(x)
# Numerical verification
def numerical_derivative(f, x, h=1e-5):
return (f(x + h) - f(x)) / h
x = 2
analytical = h_prime(x)
numerical = numerical_derivative(h, x)
print(f"Analytical: {analytical:.6f}")
print(f"Numerical: {numerical:.6f}")
Expected output:
ML connection: Computing derivatives of combined transformations during optimization.
Chain Rule for Derivatives
The chain rule handles composite functions—functions inside other functions. This is the most important derivative rule for neural networks.
Chain rule:
Or in Leibniz notation, if $\(y = f(u)\)$ and $\(u = g(x)\)$:
Intuition: "How does $\(y\)$ change with $\(x\)$? First see how $\(y\)$ changes with $\(u\)$, then see how $\(u\)$ changes with $\(x\)$, and multiply."
Example 1: $\(h(x) = (x^2 + 1)^3\)$
Let $\(u = x^2 + 1\)$, so $\(h = u^3\)$.
Example 2: $\(h(x) = e^{x^2}\)$
Let $\(u = x^2\)$, so $\(h = e^u\)$.
Python verification:
import numpy as np
# Function h(x) = (x^2 + 1)^3
def h(x):
return (x**2 + 1)**3
# Derivative using chain rule: h'(x) = 6x(x^2 + 1)^2
def h_prime(x):
return 6*x * (x**2 + 1)**2
# Numerical verification
def numerical_derivative(f, x, h=1e-5):
return (f(x + h) - f(x)) / h
x = 2
analytical = h_prime(x)
numerical = numerical_derivative(h, x)
print(f"Analytical: {analytical}")
print(f"Numerical: {numerical:.6f}")
Expected output:
ML connection: Backpropagation
Neural networks are deeply nested composite functions. Backpropagation is just the chain rule applied layer by layer:
Each $\(\frac{\partial a_i}{\partial a_{i-1}}\)$ is computed using the chain rule, propagating gradients backward through the network.
Partial Derivatives
When functions have multiple variables, we use partial derivatives to see how the function changes with respect to one variable while keeping others constant.
Notation:
How to compute: Treat all other variables as constants and differentiate normally.
Example: $\(f(x, y) = x^2y + 3xy^2\)$
Partial derivative with respect to $\(x\)$ (treat $\(y\)$ as constant):
Partial derivative with respect to $\(y\)$ (treat $\(x\)$ as constant):
Gradient vector:
The gradient combines all partial derivatives into a vector:
Python implementation:
import numpy as np
# Function f(x, y) = x^2 * y + 3*x*y^2
def f(x, y):
return x**2 * y + 3*x*y**2
# Partial derivatives
def df_dx(x, y):
return 2*x*y + 3*y**2
def df_dy(x, y):
return x**2 + 6*x*y
# Evaluate at (x=2, y=3)
x, y = 2, 3
print(f"f({x}, {y}) = {f(x, y)}")
print(f"∂f/∂x at ({x}, {y}) = {df_dx(x, y)}")
print(f"∂f/∂y at ({x}, {y}) = {df_dy(x, y)}")
# Gradient vector
gradient = np.array([df_dx(x, y), df_dy(x, y)])
print(f"Gradient ∇f at ({x}, {y}) = {gradient}")
Expected output:
ML connection: Gradient descent computes partial derivatives of the loss function with respect to each model parameter:
Each parameter is updated based on its partial derivative.
What is an Integral?
An integral is the reverse of a derivative. While derivatives measure rates of change, integrals measure accumulation or total area under a curve.
Two types:
- Indefinite integral (antiderivative): Find a function whose derivative gives you the original function
- Definite integral: Calculate the actual area under the curve between two points
Notation:
The $\(\int\)$ symbol means "integrate," and $\(dx\)$ indicates we're integrating with respect to $\(x\)$.
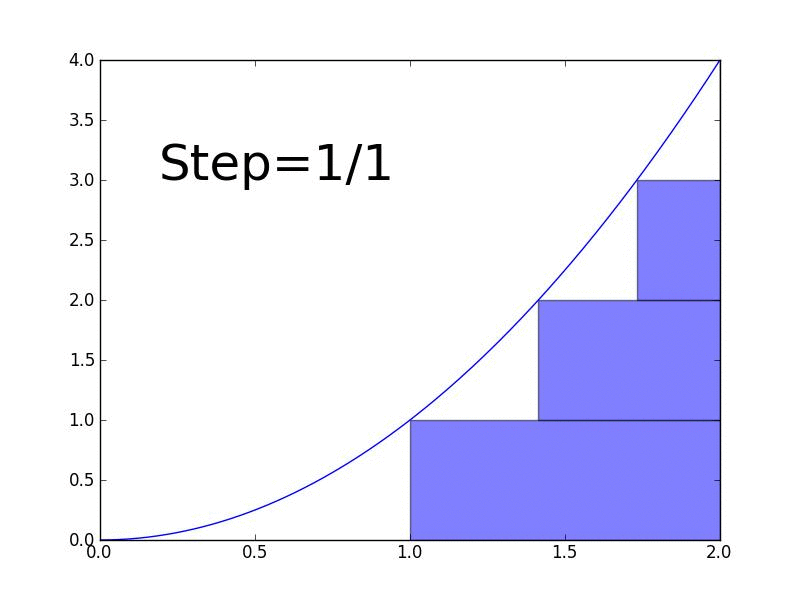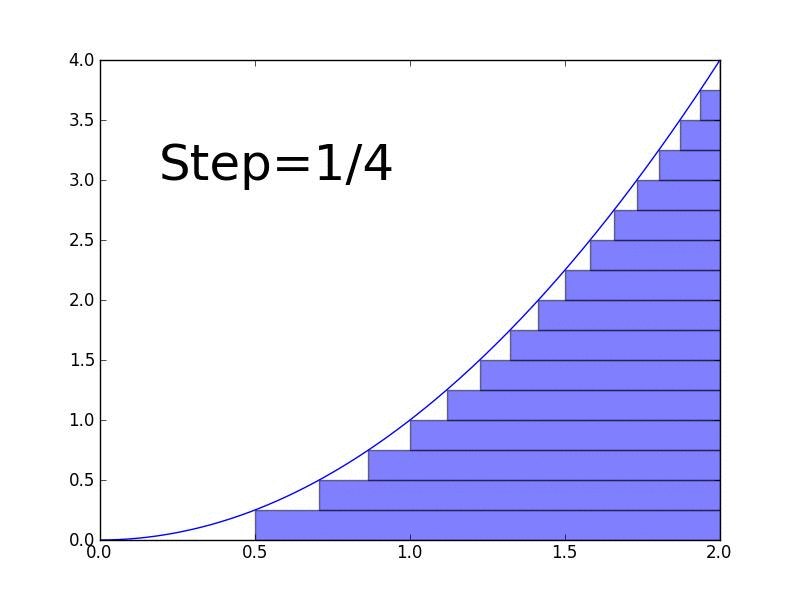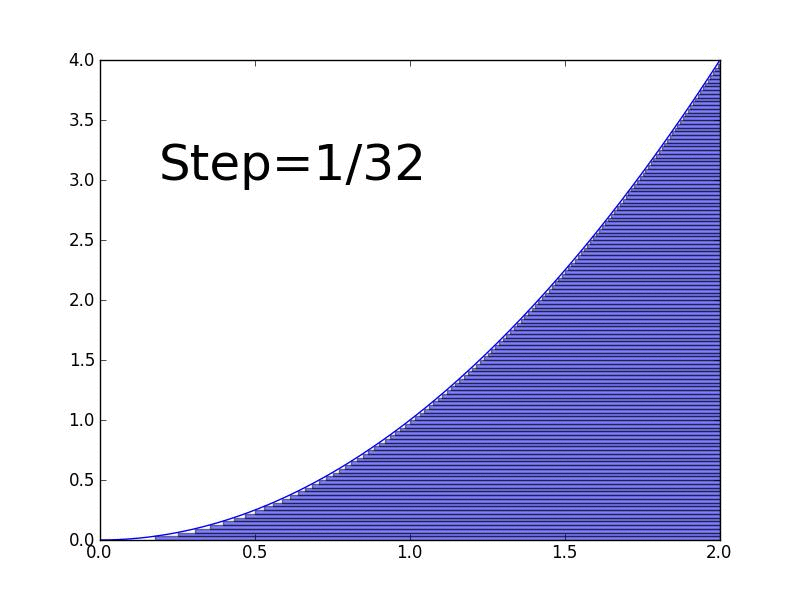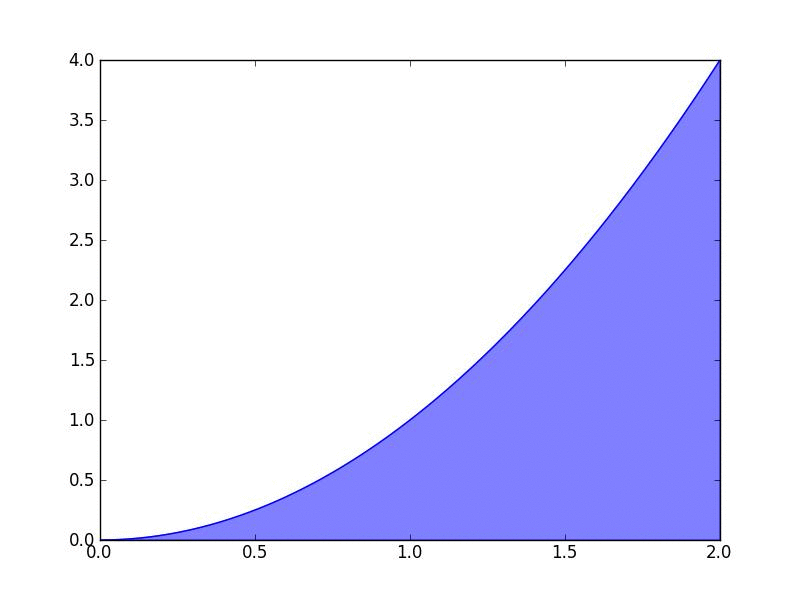
Why integrals matter in ML:
- Computing probabilities (area under probability density functions)
- Calculating expected values
- Optimization (finding cumulative sums)
- Analyzing convergence
Indefinite Integrals
An indefinite integral finds the antiderivative—a function $\(F(x)\)$ such that $\(F'(x) = f(x)\)$.
General form:
The $\(+ C\)$ is the constant of integration (because derivatives of constants are zero, we can't determine $\(C\)$ from integration alone).
Basic integration rules:
Constant:
Power rule:
Examples:
-
\[\int x^2 \, dx = \frac{x^3}{3} + C\]
-
\[\int x^5 \, dx = \frac{x^6}{6} + C\]
-
\[\int 1 \, dx = x + C\]
Reciprocal (special case when $\(n = -1\)$):
Exponential:
Verification with derivatives:
import sympy as sp
# Define variable
x = sp.Symbol('x')
# Function to integrate
f = x**2
# Compute indefinite integral
F = sp.integrate(f, x)
print(f"∫{f} dx = {F} + C")
# Verify by taking derivative
derivative = sp.diff(F, x)
print(f"Derivative of {F}: {derivative}")
print(f"Matches original? {derivative == f}")
Expected output:
Definite Integrals
A definite integral computes the exact area under a curve between two limits $\(a\)$ and $\(b\)$.
Notation:
Fundamental Theorem of Calculus:
Where $\(F(x)\)$ is any antiderivative of $\(f(x)\)$.
Example: $\(\int_0^2 x^2 \, dx\)$
- Find antiderivative: $\(F(x) = \frac{x^3}{3}\)$
- Evaluate at limits: $\(F(2) - F(0) = \frac{2^3}{3} - \frac{0^3}{3} = \frac{8}{3} - 0 = \frac{8}{3}\)$
So $\(\int_0^2 x^2 \, dx = \frac{8}{3} \approx 2.667\)$.
Python verification:
import numpy as np
from scipy import integrate
# Function to integrate
def f(x):
return x**2
# Definite integral from 0 to 2
result, error = integrate.quad(f, 0, 2)
print(f"∫₀² x² dx = {result:.6f}")
# Analytical solution
analytical = (2**3)/3 - (0**3)/3
print(f"Analytical result: {analytical:.6f}")
Expected output:
ML connection: Probability
Probability density functions (PDFs) integrate to 1 over their domain:
To find the probability that $\(X\)$ falls in range $\([a, b]\)$:
Double Integrals
Double integrals extend integration to functions of two variables, computing volume under a surface.
Notation:
How to compute:
- Integrate with respect to $\(y\)$ first (treat $\(x\)$ as constant)
- Then integrate the result with respect to $\(x\)$
Example: $\(\int_0^1 \int_0^2 xy \, dy \, dx\)$
Step 1: Inner integral (with respect to $\(y\)$):
Step 2: Outer integral (with respect to $\(x\)$):
So $\(\int_0^1 \int_0^2 xy \, dy \, dx = 1\)$.
Python verification:
from scipy import integrate
# Function f(x, y) = x*y
def f(y, x): # Note: order is reversed for dblquad
return x * y
# Double integral
result, error = integrate.dblquad(f, 0, 1, 0, 2)
print(f"∫∫ xy dy dx = {result:.6f}")
Expected output:
ML connection: Expected values of functions over joint probability distributions use double integrals:
Quick Reference for Calculus Operations
| Concept | Notation | Formula/Rule | ML Application |
|---|---|---|---|
| Summation | $\(\sum_{i=1}^n a_i\)$ | $\(a_1 + a_2 + \cdots + a_n\)$ | Loss functions, batch gradients |
| Product | $\(\prod_{i=1}^n a_i\)$ | $\(a_1 \times a_2 \times \cdots \times a_n\)$ | Probability of independent events |
| Derivative | $\(f'(x)\)$ or $\(\frac{df}{dx}\)$ | $\(\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\)$ | Gradient descent |
| Power rule | $\(\frac{d}{dx}x^n\)$ | $\(nx^{n-1}\)$ | Computing gradients |
| Sum rule | $\(\frac{d}{dx}[f+g]\)$ | $\(f' + g'\)$ | Additive loss functions |
| Product rule | $\(\frac{d}{dx}[f \cdot g]\)$ | $\(f'g + fg'\)$ | Combined transformations |
| Chain rule | $\(\frac{d}{dx}f(g(x))\)$ | $\(f'(g(x)) \cdot g'(x)\)$ | Backpropagation |
| Partial derivative | $\(\frac{\partial f}{\partial x}\)$ | Derivative treating other vars constant | Multi-parameter optimization |
| Indefinite integral | $\(\int f(x) \, dx\)$ | $\(F(x) + C\)$ where $\(F' = f\)$ | Finding antiderivatives |
| Definite integral | $\(\int_a^b f(x) \, dx\)$ | $\(F(b) - F(a)\)$ | Probability calculations |
Summary & Next Steps
Key accomplishments: You've learned summation and product notation for expressing series, understood derivatives as rates of change and their computation rules, mastered the chain rule essential for backpropagation, computed partial derivatives for multivariate optimization, and understood integrals for probability and accumulation.
Best practices:
- Verify derivatives numerically when implementing custom functions
- Use automatic differentiation (like PyTorch's autograd) in production, but understand the math
- Check dimensions when computing gradients to catch errors early
- Visualize functions and their derivatives to build geometric intuition
- Start with simple examples before tackling complex nested functions
Connections to ML:
- Gradient descent: Uses derivatives to find parameter updates: $\(w := w - \alpha \frac{\partial L}{\partial w}\)$
- Backpropagation: Applies chain rule layer-by-layer to compute gradients in neural networks
- Loss functions: Derivatives show which direction reduces error
- Probability: Integrals compute cumulative distributions and expected values
- Optimization: Second derivatives (curvature) help adaptive learning rate methods
External resources:
- 3Blue1Brown: Essence of Calculus - visual and intuitive calculus explanations
- Khan Academy: Calculus - comprehensive practice problems
- MIT OpenCourseWare: Single Variable Calculus - rigorous mathematical foundation
Next tutorial: Apply these calculus concepts to understand gradient descent optimization and implement a simple neural network from scratch using derivatives.